Regressing the Log Function with Neural Networks

What if you were given $ln(x+y) = 4.6$ and asked to guess $x$ and $y$, would you be able to provide a satisfying pair of $(x,y)$? Sure you can; one could do $e^{4.6}$ and then choose $x$ and $y$ to their liking. But the issue is that, if $x$ and $y$ are predefined and we only get $ln(x+y)$, then there is no mathematical rule to get back $x$ and $y$. The only way would be brute forcing (trying all pairs of $x$ and $y$ until we get the correct one) and an oracle then tells us whether our chosen $x$ and $y$ is correct. But can neural networks figure this out if we supervise them?

In this series of experiments, we tested to see if fully connected neural networks (FCNs) can undo a logarithm and an addition to predict $x$ and $y$ from $ln(x+y)$. Hence, the input is a single number i.e. $ln(x+y)$ and the outputs are $x$ and $y$. The FCNs had one or two hidden layers, each with a number of nodes of 10, 50, 100, 500 or 1000 and even 50,000. Most experiments were done for 500 epochs, but a few for 1000 epochs, which will be mentioned below. The Adam optimizer was used and a learning rate of 0.001 worked best.

For evaluation, the $R^2$ score and the output residuals were observed, since this is a regression task. The $R^2$ score can range from large negative numbers (badly fitted models) to a maximum perfect score of 1. So, models with $R^2$ scores close to 1 are skilled models. The output residual is simply the absolute difference between the prediction and the label, so lower is better.

The dataset was generated, where numbers between 0 and a maximum were generated uniformly and randomly, then the $ln(x+y)$ input was calculated and the $(x,y)$ were used as labels. Then these values were normalized by their respective maxima. The dataset consisted of 10,000 of these input- output sets and the maximum $x$ or $y$ were between 100 and 1000.

The results reveal that these FCNs are not good at reversing the logarithm and addition, with the best model having a $R^2$ score of 0.55.

For FCNs with one hidden layer, having more nodes leads to better $R^2$ scores, but not by a big margin. Hence, having 50,000 nodes (red line) gave the maximum $R^2$ score of 0.55, but in spite of training for 1000 epochs, the score plateaued very early.

For FCNs with two hidden layers, increasing network size doesn’t improve $R^2$ score. In fact, the $[500, 500]$ nodes network had the maximum score (red line), while even bigger network sizes of, say, $[1000, 1000]$ performed a little worse. But even here, the score levels off early at 0.55.

The output residuals had an amazing distribution: a bell shaped curve, which is a pretty neat Gaussian. This means the predicted $x$ and $y$ are off by a certain amount in most cases.

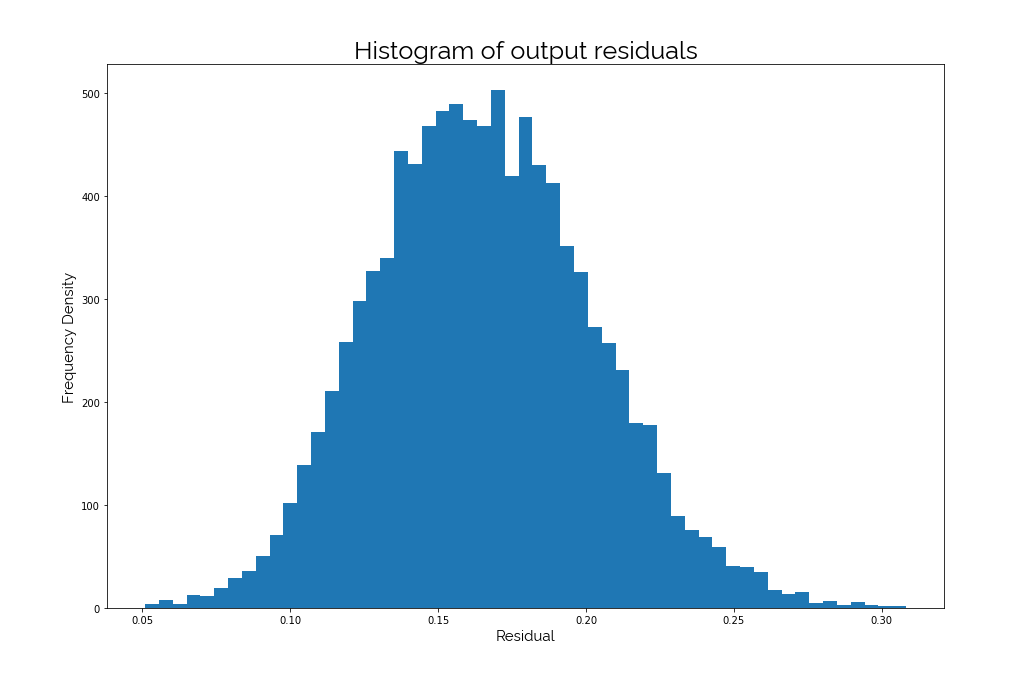
These experiments conclude that FCNs will not be effective when mapping relationships that involve reserving a logarithm and addition.

This experiment was inspired by Multiplying large numbers with Neural Networks and uses the code from there as well.

The code and experimental data for these results can be found in this repo.