Computing Greeks for American Options Part 2

In part 1 of this series we discussed the Binomial Options Pricing model (BOPM). We showed how to build the underlying stock price tree and how to compute the option prices at the expiration date (useful for European options). Now, two things are missing: Computing option prices at dates before the expiration, and computing greeks based on a BOPM.

Now, computing option prices is done as follows. First, we need a helper constant, the probability $p$:

$p = \frac{e^{rt} - d}{u - d}$

where $u$ and $d$ are defined as the upward and downward implied volatility (cf. part 1).

This is also where the binomial part of the BOPM comes in: $p$ stands for the probability of an upward move (and conversely, $1-p$ is the probability of a downward move). Anyone who had an introduction to statistics will quickly see that this can be related to the binomial distribution. To compute the option price of some given date, we define the value of it as its expected value in the future (but discounted by the risk free rate $r$, i.e. the US Treasury 10y yield from part 1). Since we have a tree with discrete time steps, the value of an option at some time step is the value of both outcomes (upward or downward move) weighed by their respective probabilities. Thus, to compute all the option prices, we have to go backwards from the leaf nodes of the tree up to the root.

Note that in our example, $p = \frac{e^{0.015 * 0.125} - 0.976}{1.025 - 0.976} = 0.532$. So the chance of the upward move is roughly $53\%$. For each node in the tree that is not a leaf node, the following is computed:

$e^{-rt} (p*O_u + (1-p)*O_d)$

where $O_u$ is the option price in the upward move and $O_d$ is the option price in the downward move. Note that at the beginning, the leafs are already computed as defined in part 1. The resulting options prices (if held until expiration) at 4 different time steps for 6 months (as per our hypothetical example) are shown in the following Figure.

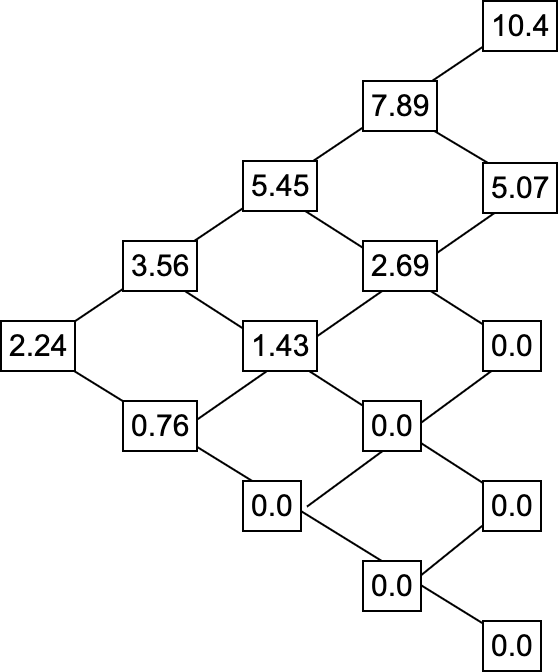
Since this is a call option, any time the underlying stock loses value, the option loses any intrinsic worth (any time the tree shows a value of $0.0$). Note that dividend yield was excluded in the discussion and computations above.

One last consideration has to be made for American style options: If exercised early, and the exercise value is larger than the binomial option price, the actual option price is the exercise value. For a call option, the exercise value is computed as stock_price at time step n - strike_price.